10205. Автомагистрали
Островное государство
Флатопия идеально плоское. К сожалению, во Флатопии очень плохая система
автомобильных дорог. Правительство Флатопии осознает эту проблему и уже
построило ряд автомагистралей, соединяющих некоторые из наиболее важных
городов. Тем не менее, есть города, до которых нельзя добраться по шоссе.
Необходимо построить еще автомагистрали так, чтобы можно было проехать между
любой парой городов, не выезжая за пределы системы магистралей.
Города во Флатопии
пронумерованы с 1 до n, координаты города i задаются координатами (xi, yi). Каждое шоссе соединяет ровно два города. Все автомагистрали (как исходные, так и
строящиеся) проходят по прямым линиям, поэтому их длина равна декартову
расстоянию между городами. Все шоссе можно использовать в обоих направлениях.
Автомагистрали могут свободно пересекать друг друга, но водитель может
переезжать с одной магистрали на другую только в городе, который расположен в
конце этих магистралей.
Правительство Флатопиан
хочет минимизировать затраты на строительство новых шоссе. Однако они хотят
гарантировать, что до каждого города можно добраться по шоссе из любого
другого. Поскольку Флатопия плоская, стоимость шоссе всегда пропорциональна его
длине. Поэтому самая дешевая система автомагистралей будет та, которая минимизирует
общую их длину.
Вход. Первая строка содержит
количество тестов. Затем идет пустая строка и наборы данных, разделенные пустой
строкой. Каждый тест состоит из двух частей. В первой части описаны все города
страны, а во второй части – все уже построенные автомагистрали.
Первая строка каждого теста
содержит количество городов n (1 ≤ n ≤ 750). Каждая из следующих n строк содержит по два целых
числа xi и yi – координаты i - го города (для i от 1 до n).
Абсолютное значение координат не превышает 10000. Каждый город имеет
уникальное местоположение.
Следующая строка содержит
количество существующих автомагистралей m (0 ≤ m ≤ 1000). Каждая из следующих m строк содержит номера городов, которые уже соединены автомагистралью.
Каждую пару городов соединяет не более одного шоссе.
Выход. Для каждого теста выведите
одну строку для каждой новой магистрали, которые необходимо построить для
соединения всех городов. При этом минимизируйте общую длину новых магистралей.
Каждая магистраль должна быть представлена в виде номеров городов, которые она
соединяет.
Если новых магистралей
строить не нужно (все города уже соединены), выведите предложение “No new highways need”.
Между тестами следует
выводить пустую строку.
|
Пример входа |
Пример выхода |
|
1 7 3 3 6 2 8 1 6 0 2 0 0 1 0 3 3 4 2 5 2 6 7 |
1 7 6 5 2 3 |
РЕШЕНИЕ
графы –
алгоритм Прима
Анализ алгоритма
Выделим компоненты связности по уже
имеющимся связям, воспользовавшись системой непересекающихся множеств. Запустим
алгоритм Прима. Если релаксируется ребро, соединяющее вершины из одной
компоненты связности, считаем его длину равной нулю. При добавлении ребра в
минимальный остов объединяем в одно множество вершины на его концах.
Пример
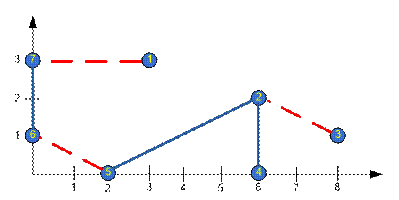
Рассмотрим
пример, приведенный в условии. Синим обозначены уже построенные магистрали. Красным –
которые будут построены.
Реализация алгоритма
Объявим
глобальные массивы. Координаты городов храним в (x[i], y[i]). Значение used[i]
= 1, если вершина i включена в остов. Значение
dist[i] хранит наименьшее расстояние от вершины, не включенной
еще в остов, до текущего минимального остова. Значение prev[i]
содержит вершину из минимального остова, к которой лучше будет подсоединить
вершину i. Когда вершина i войдет в минимальный
остов, то ребро (prev[i], i)
будет ему принадлежать.
#define MAX 751
#define INF 0x3F3F3F3F
int mas[MAX], x[MAX], y[MAX], used[MAX], dist[MAX], prev[MAX];
Функция Repr возвращает
представителя вершины n.
int Repr(int n)
{
if (n == mas[n]) return n;
return mas[n] = Repr(mas[n]);
}
Функция Union объединяет
множества, содержащие вершины x и y.
int Union(int x, int y)
{
x = Repr(x); y = Repr(y);
mas[x] = y;
return (x != y);
}
Функция dist2 вычисляет квадрат расстояния между городами i и j.
int dist2(int i, int j)
{
return (x[j] - x[i])*(x[j] - x[i]) + (y[j] - y[i])*(y[j] - y[i]);
}
Функция Prim реализует алгоритм
Прима.
void Prim(void)
{
Инициализируем
массивы.
memset(dist, 0x3F, sizeof(dist));
memset(used, 0, sizeof(used));
memset(prev, -1, sizeof(prev));
Начинаем строить минимальный остов с вершины 1. Инициализируем dist[1] = 0, used[1] = 1.
int i, j, cur = 1;
dist[cur] = 0;
used[cur] = 1;
Совершаем n – 1 итерацию. На каждой итерации в остов добавляем одну вершину (так что в
остов еще следует добавить n – 1 вершин).
for (i = 1; i <
n; i++)
{
Текущей вершиной является cur. Перебираем ребра (cur, j) и пересчитываем значение dist[j]. Таким образом dist[j] хранит текущее кратчайшее расстояние от вершины j до текущего минимального остова.
for (j = 1; j <=
n; j++)
{
if (!used[j])
{
Если вершины cur и j лежат в одной
компоненте связности, то расстояние между ними положим равным 0 (dist[j]
= 0).
if (Repr(cur) ==
Repr(j))
{
dist[j] = 0;
prev[j] = cur;
}
else if (dist2(cur, j)
< dist[j])
{
dist[j] =
dist2(cur, j);
prev[j] = cur;
}
}
}
Ищем ребро наименьшей длины, которое будет включено в
остов. Для этого ищем такое наименьшее dist[j], что вершина j еще не принадлежит остову (used[j] = 0). Номер вершины с наименьшим dist[j] заносим в cur (она становится текущей).
int min = INF;
cur = -1;
for (j = 1; j <=
n; j++)
if (!used[j]
&& (dist[j] < min))
{
min = dist[j];
cur = j;
}
Вершина cur включается в
остов. В остов также
включается ребро (prev[cur], cur).
used[cur] = 1;
Если вершины cur и prev[cur] еще не связаны дорогами, то строим дорогу (prev[cur], cur). Объединяем множества, содержащие вершины cur и prev[cur].
if (Repr(cur) !=
Repr(prev[cur]))
{
printf("%d
%d\n", prev[cur], cur);
Union(prev[cur],
cur);
}
}
}
Основная
часть программы. Обрабатываем tests тестов.
scanf("%d", &tests);
while (tests--)
{
Читаем
входные данные.
scanf("%d", &n);
for (i = 1; i <= n; i++)
scanf("%d %d", &x[i],
&y[i]);
Инициализируем систему непересекающихся множеств.
for (i = 1; i <= n; i++) mas[i] = i;
scanf("%d", &m);
Для каждого ребра (u, v) объединяем множества, содержащие u и v. В переменной cnt подсчитываем количество ребер, использованных
для их объединения.
cnt = 0;
for (i = 0; i < m; i++)
{
scanf("%d %d", &u,
&v);
cnt += Union(u, v);
}
Если cnt = n – 1,
то изначально имеющиеся автомагистрали образуют связный граф. Новых шоссе
строить не надо.
if (cnt == n - 1)
puts("No new highways need");
else
Prim();
Между тестами выводим пустую строку.
if (tests) puts("");
}